1-6 その他のコード(和音)と転回形
~もくじ~
その他のコード
1-5 コード(和音)とはで出てこなかったコードを見ていきましょう。コードの基本は3度音程の堆積ですが、中にはそれに当てはまらない特殊なコードがあります。
sus4(サスペンデッド・フォース)
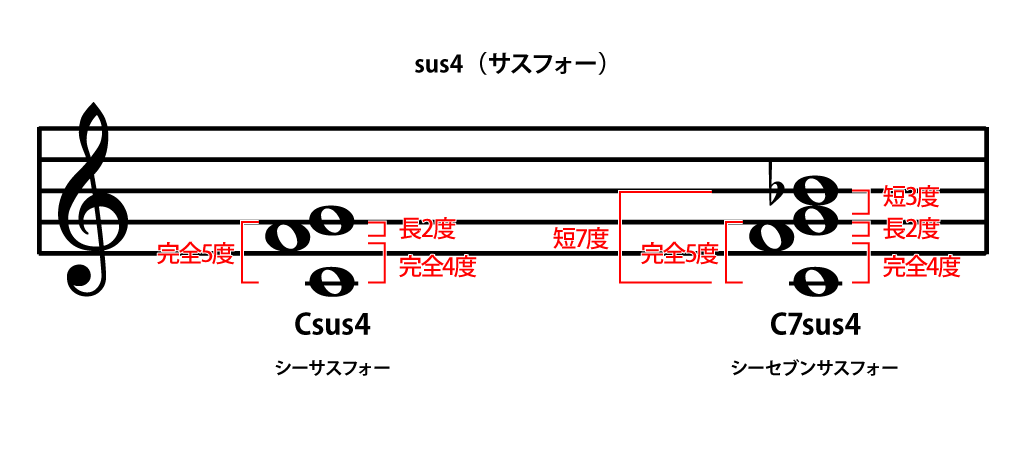
サスペンデッドフォースを略して「サスフォー」と呼ばれます。
3度堆積和音の3度の音をなくし、4度の音を加えています。
suspended(サスペンデッド)には「吊るされた」という意味があり、「3度の音を4度に吊り上げた」とイメージするとわかりやすいと思います。洋服でもサスペンダーってのがありますもんね。
不協和音程の長2度を含んだコードです。
6(シックス)
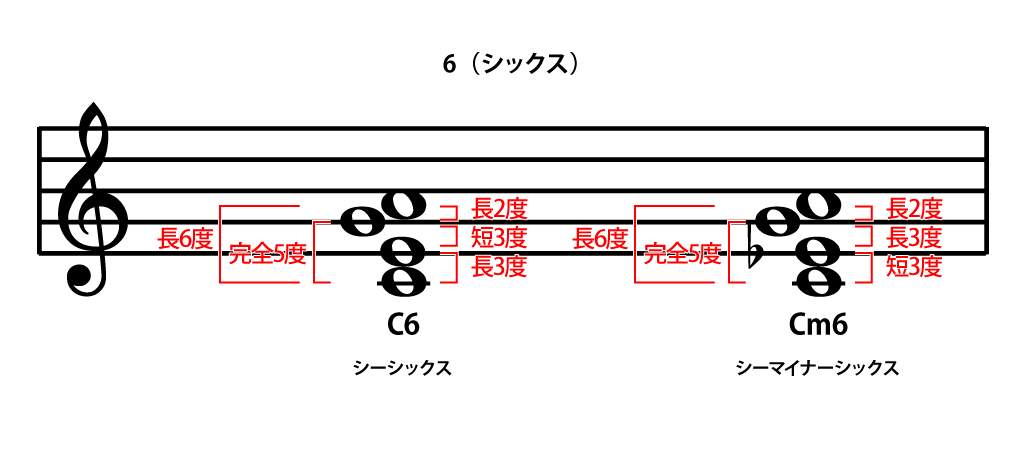
セブンスコードの7度を6度にしたコードです。長6度音程が加わります。短6度を重ねると短2度(半音)ができてしまうので「6」は長6度のみです。
長6度は9半音で、減7度と同じ音程になります。減7度といえばdim7が思い出されますが、短3度の積み重ねであり、減5度が含まれていたことを考えると全く違ったコードです。
add(アド)とomit(オミット)
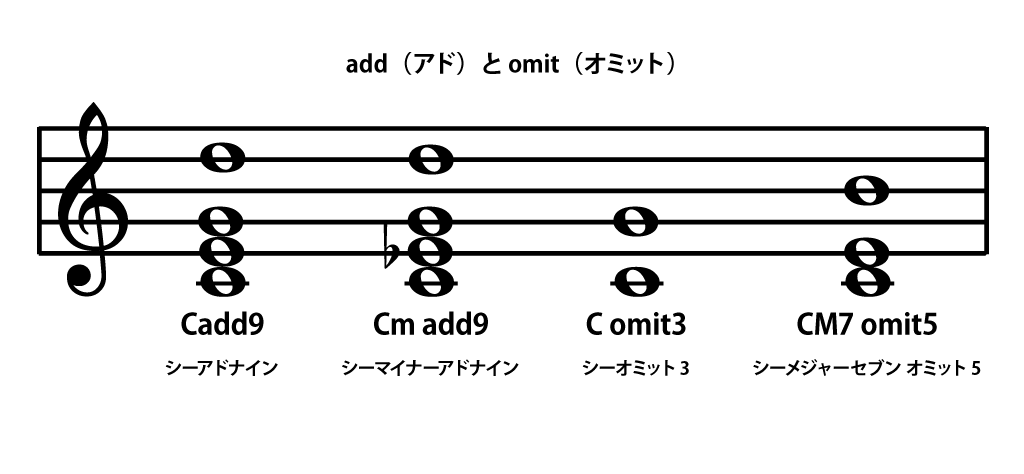
add(アド)は「付け加える」、omit(オミット)は「省く」という意味の英語です。
addはadd9(アドナイン)がよく使われます。図の1番左「シーアドナイン」の場合、Cトライアドに長9度のレが加えられているのでシーアドナイン。
もし「シ」の音も存在していたらCM7(9)ですね。
9度は「1オクターヴ+2度」と考えられるので「add9」を「add2」と表す人もいます。
addの反対にomitは省くので、「C omit3」とすると、構成音は「ドミソ」から3度の「ミ」を省いて「ドソ」ということになります。
Cにomitをつけると結果にコミットしそうになってしまいますが、コミットのスペルはcommitです。commitは「ゆだねる、約束する」と言った意味があります。
「結果にコミットする」ってのは「結果を約束する」ってことなのでしょうか?余談。
あと、ギターにはルートと5度の音を力強く鳴らす「パワーコード」というものがあります。パワーコードは音楽理論というよりはギターの奏法の1つといった感じなので「C omit3」とはまた違った意味合いです。
分数コード(オンコード)
「C/B」「C on B」のような表記を見かけることもあると思います。これは「分数コード」(オンコード)と呼ばれるもので、スラッシュは分数を表しています。
「C/B」の場合、「ビーぶんのシー」や「シー オン ビー」のように読みます。「シー オン ビー」の方が一般的なようです。
分数コードはルート以外の音をベース音(最低音)にしたい時に用います。「C/B」とした場合は、C(ド・ミ・ソ)よりも低音域に「シ」をベース音として加えます。オクターヴ以上離れたベース音を加える場合もあります。
「/」スラッシュの左側(分子)がコードの本体で、右側(分母)が加えるベース音という部分を間違えなければ大丈夫だと思います。
コードの転回形
ここまででほぼ全てのコードが表せると思います。中には捻くれたコードが出てくることもあるかもしれませんが、その時はその時ということで。
一つ覚えておかないといけないのがコードの転回形です。コードの基本は、ルートを基準に3度、3度と音を重ねていくことでしたが、実は音の順番を入れ替えても良いことになっています。つまり、コードを形作るのは構成音であって、音がオクターヴ上下してもコード自体は同じコードです。
ちょっと説明がアレなので図を見るほうが早いですね。

「基本形」が一般的なコードです。転回形はベース音(1番低い音)が何かという基準で第○転回形と名前がつけられています。
CM7の場合は、第3音のミがベース音になれば第1転回形、第5音のソがベース音になれば第2転回形、第7音のシがベース音になると第3転回形と呼びます。
一番低い音をベース音と言いますが、「ルートは何か?」と聞かれると、それはC(ド)のままです。
転回すると何のコードがわかりにくくなりますが、基本形になるように3度・3度と積み重なるように音の配置を変えてあげれば見慣れたコードの形が現れると思います。
表記の仕方は、先程の分数コードと同じで、スラッシュの左側にコード、右側にベース音を記します。分数コードとの違いは、分数コードの場合はコード構成音以外の音がベース音になることもあるという点です。ですので「転回形」は分数コードの一種であると言えると思います。
コードは構成音が基準で決められていますので、最低音から最高音が2オクターヴや3オクターヴにまたがってもコードはコードです。ギターなど1つの楽器でオクターヴのかけ離れた音を出すことは困難ですが、オーケストラのように複数の楽器を使えば広い音域の音を出すことが可能です。
それらの音をまとめるとなんらかのコードにはなっていると思います。
転回形の度数
「コードを転回すると度数がおかしくなってしまうのでは?」
というのが疑問だと思います。先程の図に度数を加えてみました。
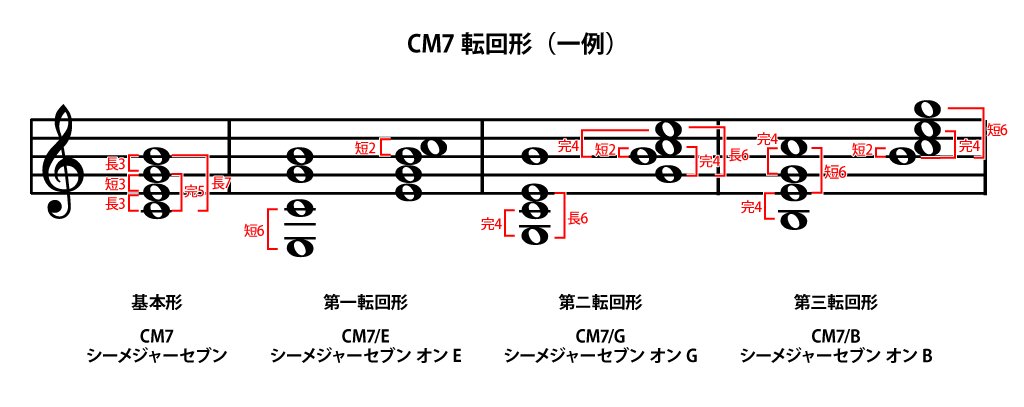
1番左、基本形は見慣れた度数が並んでいます。
第一転回形、左のコード、ミ-ソは1オクターヴ+短3度、ミ-シは1オクターヴ+完全5度と考えれば良いので問題ないです。問題はミ-ドが短6度になっている点です。
ミ-ドの短6度に対して、転回前のド-ミは長3度です。
ここで以前の度数と半音の関係という図を思い出していただきたいのですが…
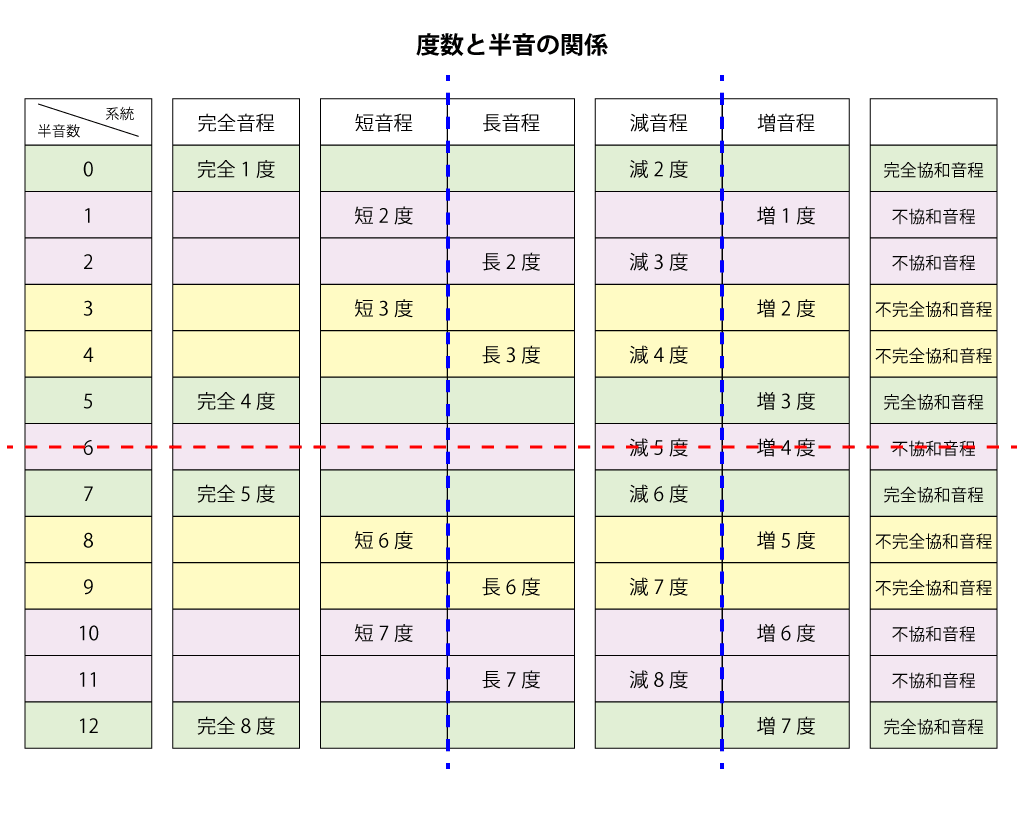
こいつです。
以前の図に線を引いてみたのですが、赤線のところで上下対称に「完全協和音程」「不完全協和音程」「不協和音程」が逆の並びになっていると思います。
そして、完全音程の配置も赤線のところで対称に配置されています。完全1度の反対の位置に完全8度、完全4度の反対の位置に完全5度。
さらに、長短系や増減系は赤線+青線で対称に配置されていると思います。短2度の対角の位置に長7度といった具合です。
つまり、それぞれの対になっている音程は完全協和音程なら完全協和音程、不完全協和音程なら不完全協和音程、不協和音程なら不協和音程になっていて、極めて関係性の深い、よく似た響きを持っていると想像できます。
先程の第一転回形のミ-ド短6度とド-ミ長3度の関係を見てみると、丁度逆の位置になっているので同じ不完全協和音程、そしてよく似た響きを持っているということになります。
転回音程は必ずこの法則が成り立ち、必ず対象の位置にきます。表にしてみました。
| 音程の種類 | 度数 |
| 完全 ←→ 完全 | 1度 ←→ 8度 |
| 長 ←→ 短 | 2度 ←→ 7度 |
| 増 ←→ 減 | 3度 ←→ 6度 |
| 重増 ←→ 重減 | 4度 ←→ 5度 |
元の音程が完全4度なら転回音程は完全5度、長2度なら短7度、増4度なら減5度といった感じです。
9-元の音程=転回音程
という式でも表せると思います。
上の「CM7転回形(一例)」の図にいろいろなパターンがありますので試してみてください。全て法則に当てはまると思います。
このことから、音を転回させても和音の響きは保たれるということがわかると思います。完全協和音程を転回したからといって不協和音程になることはありません。
ただ、理論的に似たような響きになることは間違いありませんが、だからといってなんでも自由に転回させて良いかと言うとそうでもありません。似たような響きだけど違う響きだということも事実です。
このあたりは感性の部分になるので難しいですが、例えば長7度を不快と感じなくて短2度は不快と感じる人もいるでしょうし、完全5度と完全4度では印象も違うと思います。
他の和音との兼ね合いや、音の流れによっても感じ方は変わってくると思いますので、その中でどういった音を転回し、チョイスしていくのかというのが作曲の醍醐味なのではないかと思います。